symmetrischeFunktionPunktsymmetrie zum Ursprung (ungerade Funktion) bzw.
Achsensymmetrie zur y-Achse (gerade Funktion) einer reellwertigen Funktion
Sei  eine Menge mit der Eigenschaft, dass für alle eine Menge mit der Eigenschaft, dass für alle 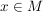 auch auch 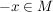 gelte. gelte.
Sei 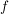 eine reellwertige Funktion mit dem Definitionsbereich eine reellwertige Funktion mit dem Definitionsbereich 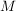 . .
Die Funktion 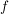 heißt: heißt:
- punktsymmetrisch zum Ursprung (oder ungerade) (auf 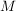 ), falls für alle ), falls für alle 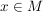 die Gleichung die Gleichung  gilt gilt
- achsensymmetrisch zur 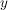 -Achse (oder gerade) (auf -Achse (oder gerade) (auf 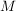 ), falls für alle ), falls für alle 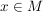 die Gleichung die Gleichung 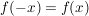 gilt. gilt.
Beispiele.
1.) Die Funktion 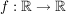 definiert durch definiert durch 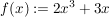 ist ungerade. Es gilt nämlich für alle ist ungerade. Es gilt nämlich für alle 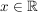 : :
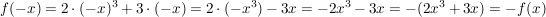 . .
2.) Die Funktion  ![$ [-3;3] \cap \IZ $ $ [-3;3] \cap \IZ $](/teximg/5/0/00387205.png) 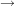 ![$ [-1000;1000] $ $ [-1000;1000] $](/teximg/2/7/00389072.png) definiert durch definiert durch 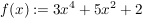 ist gerade. Es gilt nämlich für alle ist gerade. Es gilt nämlich für alle ![$ x \in [-3;3] $ $ x \in [-3;3] $](/teximg/7/0/00387207.png) : :
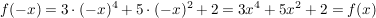 , und damit insbesondere: , und damit insbesondere:
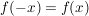 ![$ \forall x \in ([-3;3] \cap \IZ) $ $ \forall x \in ([-3;3] \cap \IZ) $](/teximg/9/0/00387209.png) . .
3.) Die Funktion 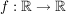 definiert durch definiert durch 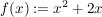 ist weder gerade noch ungerade. ist weder gerade noch ungerade.
Es gilt nämlich einerseits:

(etwa weil 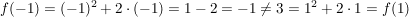 ) (d.h. ) (d.h. 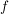 ist nicht gerade), ist nicht gerade),
und andererseits:

(etwa weil 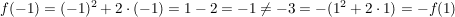 (d.h. (d.h. 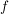 ist nicht ungerade). ist nicht ungerade).
4.) Ist 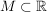 eine Menge mit der Eigenschaft, dass für alle eine Menge mit der Eigenschaft, dass für alle 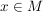 auch auch 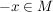 gilt, gilt,
und ist 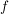 eine Funktion mit dem Definitionsbereich eine Funktion mit dem Definitionsbereich 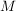 , ,
die sowohl gerade als auch ungerade ist, so ist 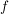 auf auf 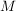 die Nullfunktion. die Nullfunktion.
Denn:
Es gilt für alle 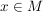 : :
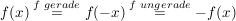
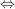

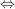
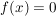 . . 
5.) Sei 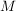 eine Menge mit der Eigenschaft, dass für alle eine Menge mit der Eigenschaft, dass für alle 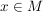 auch auch 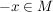 gelte. Sei ferner gelte. Sei ferner  . .
Dann gilt:
Ist 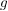 eine ungerade Funktion, so gilt eine ungerade Funktion, so gilt  . .
Denn:
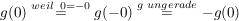
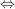
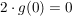
 . . 
| 