FunktionDefinition Funktion
Eine Zuordnung heißt Funktion, wenn jedem Element aus dem Definitionsbereich genau ein Element aus dem Wertebereich oder Zielbereich zugeordnet wird.
Die Zuordnungsvorschrift f(x) nennt man auch den Funktionsterm.
Bezeichnet man die Funktion mit 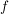 und ist und ist  eine Zahl aus dem Definitionsbereich, eine Zahl aus dem Definitionsbereich,
so nennt man 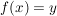 den Funktionswert der Funktion den Funktionswert der Funktion 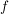 an der Stelle an der Stelle  . .
Bemerkungen.
Zwei Funktionen  und und 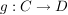 sind genau dann gleich, wenn folgende drei Bedingungen gelten: sind genau dann gleich, wenn folgende drei Bedingungen gelten:
1.) 
2.) 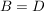
3.) 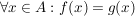 . .
Für die Gleichheit von Funktionen ist es also wesentlich, dass die Funktionen nicht nur die gleiche Funktionsvorschrift haben, sondern auch, dass sie den gleichen Definitionsbereich und den gleichen Zielbereich haben.
Eigenschaften reeller Funktionen mit Formvariablen
Mögliche Eigenschaften spezieller Funktionen
siehe auch
Kurvendiskussion, Abbildung, Graph, Relation, Parameteraufgaben, Ortskurve
Ermitteln der Funktionsgleichung von Funktionen in der SchulMatheFAQ
siehe auch bei ![Link auf "http://www.mathe-online.at/mathint/fun2/i.html" [link]](/images/popup.gif) Mathe-online.at Mathe-online.at
| 