maßerzeugendDefinition maßerzeugende Funktion/maßdefinierende Funktion/Stieltjesche Maßfunktion
Es sei
Dann heißt 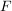 maßerzeugende Funktion (oder maßdefinierende Funktion oder Stieltjesche Maßfunktion) maßerzeugende Funktion (oder maßdefinierende Funktion oder Stieltjesche Maßfunktion)
Beispiele:
- Jede Verteilungsfunktion auf
 ist eine maßerzeugende Funktion (die Umkehrung gilt allerdings nicht). ist eine maßerzeugende Funktion (die Umkehrung gilt allerdings nicht).
Eigenschaften:
- Zu jeder maßerzeugenden Funktion
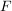 auf auf 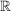 gibt es genau ein Maß gibt es genau ein Maß 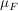 auf auf  ( ( -Algebra der Borelschen Mengen auf -Algebra der Borelschen Mengen auf 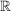 ) mit ) mit 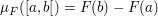
- Das von
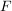 erzeugte Maß erzeugte Maß 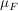 ist ein Borel-Maß. ist ein Borel-Maß.
- Zu jedem Borel-Maß auf
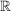 existiert eine maßerzeugende Funktion. existiert eine maßerzeugende Funktion.
Literatur: isbn3110136252
| 