EbeneDefinition Ebene
- vektorielle Darstellung einer Ebene
Schule
Jede Ebene läßt sich darstellen durch eine Gleichung folgender Form:
Hierbei ist  ein Stützvektor (Aufhängepunkt), ein Stützvektor (Aufhängepunkt), 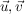 sind zwei linear unabhängige Vektoren und r,s zwei reelle Zahlen. sind zwei linear unabhängige Vektoren und r,s zwei reelle Zahlen.
Für jede reelle Zahl 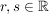 erhält man einen Punkt P und umgekehrt. erhält man einen Punkt P und umgekehrt.
Bemerkung
Eine Ebene ist durch einen Punkt und zwei (nicht parallele) Richtungen eindeutig bestimmt.
In der Ebenengleichung  lassen sich die Parameter r und s eliminieren, lassen sich die Parameter r und s eliminieren,
wenn man die drei Koordinatengleichungen aufstellt:
Es entsteht eine Gleichung nur zwischen den Variablen 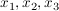 : :
mit a, b, c, d beliebige reelle Zahlen.
Diese Form der Ebenengleichung nennt man Koordinatenform oder Normalenform.
Universität
| 