Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
| argl, Tyskie84 | www.matheraum.de
Oberstufenmathematik - Analysis/Analytische Geometrie
Aufgabenblatt 8
Abgabe: Di 16.09.2008 18:00 | 09.09.2008 | | | | keine | | Aufgabe 1 | Sei 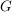 ein Monoid. Wir betrachten die folgenden Bedingungen: ein Monoid. Wir betrachten die folgenden Bedingungen:
(i) 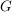 ist eine Gruppe. ist eine Gruppe.
(ii) Sind  mit mit  oder oder 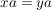 , dann gilt , dann gilt  . .
Die Implikation ''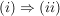 '' gilt immer. '' gilt immer.
Zeige, dass die andere Implikation '' '' für endliche Monoide auch immer gilt. Gib weiterhin ein Beispiel für einen unendlichen Monoid an, wo sie nicht gilt. '' für endliche Monoide auch immer gilt. Gib weiterhin ein Beispiel für einen unendlichen Monoid an, wo sie nicht gilt. | | Aufgabe 2 | Sei 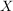 eine Menge und eine Menge und  eine Teilmenge. eine Teilmenge.
Zeige, dass die Gruppe  auf kanonische Weise als Untergruppe von auf kanonische Weise als Untergruppe von 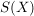 aufgefasst werden kann. aufgefasst werden kann.
Hinweis: Bei dieser Aufgabe geht es auch daraum, ueber das Wort 'kanonisch' nachzudenken  Falls euch das Wort nicht vertraut ist, schaut mal Falls euch das Wort nicht vertraut ist, schaut mal ![[]](/images/popup.gif) hier. hier. | | Aufgabe 3 | Sei 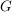 eine endliche abelsche Gruppe (multiplikativ geschrieben). Dann gilt eine endliche abelsche Gruppe (multiplikativ geschrieben). Dann gilt 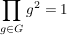 . . | | Aufgabe 4 | Sei 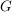 eine Gruppe mit der Eigenschaft, dass für jedes Element eine Gruppe mit der Eigenschaft, dass für jedes Element  gilt gilt  (dabei sei (dabei sei 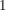 das neutrale Element der Gruppe). das neutrale Element der Gruppe).
Zeige, dass 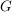 abelsch ist. abelsch ist. | | Aufgabe 5 | Sei 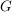 eine Gruppe und seien eine Gruppe und seien 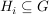 , , 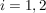 Untergruppen. Zeige, dass folgende beiden Aussagen äquivalent sind: Untergruppen. Zeige, dass folgende beiden Aussagen äquivalent sind:
(i) 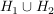 ist eine Untergruppe von ist eine Untergruppe von 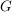 ; ;
(ii)  oder oder  . . |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|

 Falls euch das Wort nicht vertraut ist, schaut mal
Falls euch das Wort nicht vertraut ist, schaut mal