invertierbares Element
!!Definition ''invertierbares Element'
Schule
Universität
Es sei 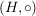 eine Halbgruppe mit neutralem Element eine Halbgruppe mit neutralem Element  . .
Ein Element 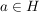 heißt linksinvertierbar (bzw. rechtsinvertierbar), wenn es ein heißt linksinvertierbar (bzw. rechtsinvertierbar), wenn es ein  gibt mit gibt mit
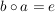 (bzw. (bzw. 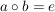 ). ).
Das Element 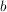 heißt ein Linksinverses (bzw. Rechtsinverses) von heißt ein Linksinverses (bzw. Rechtsinverses) von  . .
Ein Element aus  heißt __invertierbar __, wenn es sein Links- und ein Rechtsinverses besitzt. heißt __invertierbar __, wenn es sein Links- und ein Rechtsinverses besitzt.
Beispiele
1) In der Halbgruppe 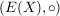 aller Abbildungen von aller Abbildungen von 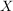 in sich sind die linksinvertierbaren Elemente genau die injektiven Abbildungen und die rechtsinvertierbaren Elemente genau die surjektiven Abbildungen (und damit die invertierbaren Elemente genau die bijektiven Abbildungen). in sich sind die linksinvertierbaren Elemente genau die injektiven Abbildungen und die rechtsinvertierbaren Elemente genau die surjektiven Abbildungen (und damit die invertierbaren Elemente genau die bijektiven Abbildungen).
Sei 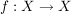 injektiv, dann prüft man sofort nach, dass injektiv, dann prüft man sofort nach, dass 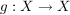 , definiert durch , definiert durch
![$ g(y):= \left\{ \begin{array}{cccc} y & , & \mbox{\scriptsize falls} & y \in X \setminus f(X),\\[5pt] x & , & \mbox{\scriptsize falls} & y=f(x), \end{array} \right. $ $ g(y):= \left\{ \begin{array}{cccc} y & , & \mbox{\scriptsize falls} & y \in X \setminus f(X),\\[5pt] x & , & \mbox{\scriptsize falls} & y=f(x), \end{array} \right. $](/teximg/9/6/00392069.png)
ein Linksinverses von 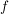 ist. Besitzt umgekehrt ist. Besitzt umgekehrt 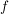 ein Linksinverses ein Linksinverses 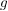 , , 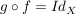 , dann folgt aus , dann folgt aus 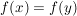 durch Anwendung von durch Anwendung von 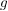
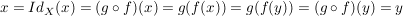 , ,
also ist 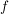 injektiv. injektiv.
Nun sei 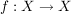 surjektiv. Dann ist jede Urbildmenge surjektiv. Dann ist jede Urbildmenge
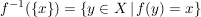
nicht leer und wir können aus jeder dieser Mengen ein Element 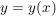 auswählen (Auswahlaxiom). Es definiert auswählen (Auswahlaxiom). Es definiert 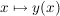 eine Abbildung, sie werde mit eine Abbildung, sie werde mit 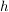 bezeichnet, für die definitionsgemäß gilt: bezeichnet, für die definitionsgemäß gilt:
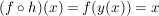 , ,
d.h. 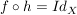 . .
Haben wir umgekehrt eine Abbildung 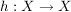 mit mit 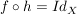 , dann gibt es zu jedem Element , dann gibt es zu jedem Element 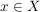 ein Element ein Element 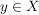 , nämlich , nämlich 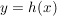 , so dass gilt: , so dass gilt:
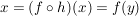 ; ;
d.h. 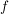 ist surjektiv. ist surjektiv.
2) Wir wollen die invertierbaren Elemente in 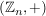 und und 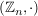 bestimmen: bestimmen:
Wegen
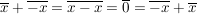
ist in 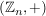 jedes Element invertierbar. jedes Element invertierbar.
Nun sei 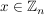 in in 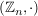 invertierbar, d.h. es gibt ein invertierbar, d.h. es gibt ein 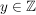 mit mit
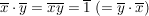 . .
Dies bedeutet:
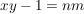 für ein für ein 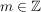 . .
Also:
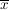 in in 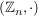 invertierbar invertierbar
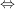 Es gibt Es gibt 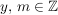 mit mit 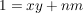
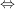  und und  sind teilerfremd. sind teilerfremd.
(Die letzte Äquivalenz ist die Aussage das Lemmas von Bézout.)
Ist  eine Primzahl, so folgt insbesondere, dass jedes Element eine Primzahl, so folgt insbesondere, dass jedes Element  in in 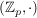 invertierbar ist. invertierbar ist.
Quelle: K. Meyberg, Algebra Teil 1, Carl Hanser Verlag, 1980, ISBN 3-446-13079-9
| 
![$ g(y):= \left\{ \begin{array}{cccc} y & , & \mbox{\scriptsize falls} & y \in X \setminus f(X),\\[5pt] x & , & \mbox{\scriptsize falls} & y=f(x), \end{array} \right. $ $ g(y):= \left\{ \begin{array}{cccc} y & , & \mbox{\scriptsize falls} & y \in X \setminus f(X),\\[5pt] x & , & \mbox{\scriptsize falls} & y=f(x), \end{array} \right. $](/teximg/9/6/00392069.png)