matheraum.de
Raum für Mathematik
Offene Informations- und Nachhilfegemeinschaft

Für Schüler, Studenten, Lehrer, Mathematik-Interessierte.
Hallo Gast! [ einloggen | registrieren ]
Startseite · Forum · Wissen · Kurse · Mitglieder · Team · Impressum
Forenbaum
^ Forenbaum
Status Hochschulmathe
  Status Uni-Analysis
    Status Reelle Analysis
    Status UKomplx
    Status Uni-Kompl. Analysis
    Status Differentialgl.
    Status Maß/Integrat-Theorie
    Status Funktionalanalysis
    Status Transformationen
    Status UAnaSon
  Status Uni-Lin. Algebra
    Status Abbildungen
    Status ULinAGS
    Status Matrizen
    Status Determinanten
    Status Eigenwerte
    Status Skalarprodukte
    Status Moduln/Vektorraum
    Status Sonstiges
  Status Algebra+Zahlentheo.
    Status Algebra
    Status Zahlentheorie
  Status Diskrete Mathematik
    Status Diskrete Optimierung
    Status Graphentheorie
    Status Operations Research
    Status Relationen
  Status Fachdidaktik
  Status Finanz+Versicherung
    Status Uni-Finanzmathematik
    Status Uni-Versicherungsmat
  Status Logik+Mengenlehre
    Status Logik
    Status Mengenlehre
  Status Numerik
    Status Lin. Gleich.-systeme
    Status Nichtlineare Gleich.
    Status Interpol.+Approx.
    Status Integr.+Differenz.
    Status Eigenwertprobleme
    Status DGL
  Status Uni-Stochastik
    Status Kombinatorik
    Status math. Statistik
    Status Statistik (Anwend.)
    Status stoch. Analysis
    Status stoch. Prozesse
    Status Wahrscheinlichkeitstheorie
  Status Topologie+Geometrie
  Status Uni-Sonstiges

Gezeigt werden alle Foren bis zur Tiefe 2

Navigation
 Startseite...
 Neuerdings beta neu
 Forum...
 vorwissen
   Einstieg
   
   Index aller Artikel
   
   Hilfe / Dokumentation
   Richtlinien
   Textgestaltung
 vorkurse...
 Werkzeuge...
 Nachhilfevermittlung beta...
 Online-Spiele beta
 Suchen
 Verein...
 Impressum
Das Projekt
Server und Internetanbindung werden durch Spenden finanziert.
Organisiert wird das Projekt von unserem Koordinatorenteam.
Hunderte Mitglieder helfen ehrenamtlich in unseren moderierten Foren.
Anbieter der Seite ist der gemeinnützige Verein "Vorhilfe.de e.V.".
Partnerseiten
Weitere Fächer:

Open Source FunktionenplotterFunkyPlot: Kostenloser und quelloffener Funktionenplotter für Linux und andere Betriebssysteme
Startseite > gleichmäßig_beschleunigte_Bewegung
Foren für weitere Schulfächer findest Du auf www.vorhilfe.de z.B. Deutsch • Englisch • Französisch • Latein • Spanisch • Russisch • Griechisch
gleichmäßig_beschleunigte_Bewegung
Mach mit! und verbessere/erweitere diesen Artikel!
Artikel • Seite bearbeiten • Versionen/Autoren

gleichmäßig beschleunigte Bewegung

Bewegung in einer Dimension


Konstante Geschwindigkeit

Der einfachste Fall einer Bewegung ist, wenn ein Körper sich mit einer konstanten Geschwindigkeit bewegt. Der Körper erfährt hierbei keinerlei Beschleunigung.

$ a \ = \ 0 $

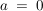
Das sogenannte "Weg-Zeit-Gesetz" der Bewegung lautet

$ x \ = \ v \cdot{} t $

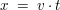
Wobei t die Zeit, v die Geschwindigkeit und x den Ort bezeichnet.


Beschleunigte Bewegung

Bei einer beschleunigten Bewegung ändert sich die Geschwindigkeit mit der Zeit.

$ a \ \not= \ 0 $

Die Momentangeschwindigkeit berechnet sich aus dem "Geschwindigkeits-Zeit-Gesetz"

$ v \ = \ v_0 + a \cdot{} t $

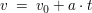
Das "Weg-Zeit-Gesetz" entspricht dem Integral des Geschwindigkeit-Zeit-Gesetzes

$ \bruch{dx}{dt} \ = \ v_0 + a \cdot{} t $

$ dx = (v_0 + a \cdot{} t) dt $

$ \integral{1 \ dx} \ = \ \integral{(v_0 + a \cdot{} t) \ dt} $

$ x \ = \ x_0 + v_0 \cdot{} t + \bruch{1}{2}\cdot{}a\cdot{}t^2 $

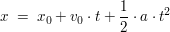
Zurück zu

MatheBank - PhysikBank - ChemieBank - Formelsammlung Physik

Erstellt: Mi 05.03.2008 von miniscout
Letzte Änderung: Mi 16.04.2008 um 14:14 von miniscout
Weitere Autoren: Loddar
Artikel • Seite bearbeiten • Versionen/Autoren • Titel ändern • Artikel löschen • Quelltext
^ Seitenanfang ^
www.unimatheforum.de
[ Startseite | Forum | Wissen | Kurse | Mitglieder | Team | Impressum ]