bedingtDefinition bedingte Wahrscheinlichkeit
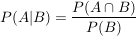
P(A|B) heißt die bedingte Wahrscheinlichkeit von A unter der Bedingung B.
Beispiel:
Aus einem Sack mit Kugeln, die mit "A","N","A","N","A","S" beschriftet sind, zieht man nacheinander vier Kugeln. Mit welcher W'keit entsteht so das Wort "ANNA" ?
Wir brauchen zuerst ein "A" aus dem noch vollen Sack:
P("A") 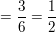
Kommt kein "A" (ebenfalls mit 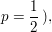 ist das Spiel aus, weil "ANNA" nicht mehr möglich ist. Haben wir aber tatsächlich ein "A" erwischt, ziehen wir die zweite Kugel. Die sollte ein "N" tragen. Das tut sie, nachdem schon ein "A" weg ist, mit ist das Spiel aus, weil "ANNA" nicht mehr möglich ist. Haben wir aber tatsächlich ein "A" erwischt, ziehen wir die zweite Kugel. Die sollte ein "N" tragen. Das tut sie, nachdem schon ein "A" weg ist, mit 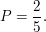 Bei Ziehung aus dem noch vollen Sack wäre natürlich Bei Ziehung aus dem noch vollen Sack wäre natürlich 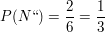 gewesen. Deshalb schreibe ich für die W'keit eines "N" nach einem "A" nicht einfach P("N"), sondern gewesen. Deshalb schreibe ich für die W'keit eines "N" nach einem "A" nicht einfach P("N"), sondern
P("AN" | "A") 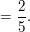
Dies ist nun eben eine bedingte Wahrscheinlichkeit. In der Klammer schreibt man hinter dem vertikalen Strich das vorausgesetzte (vorangegangene) Ereignis hin. Nachher geht es für die dritte Kugel so weiter:
P("ANN" | "AN") 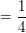
und für die vierte:
P("ANNA" | "ANN") 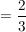
Für die eigentlichen (nicht "bedingten") Wahrscheinlichkeiten erhalten wir dann der Reihe nach:
P("A") 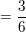
P("AN") = P("A") *P("AN" | "A") 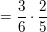
P("ANN") = P("AN")*P("ANN" | "AN") 
P("ANNA") = P("ANN")*P("ANNA" | "ANN") 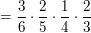
Um noch die Schreibweise mit der Schnittmenge von Ereignissen ins Spiel zu bringen:
Das kombinierte Ereignis "AN" kommt genau dann zustande, wenn zuerst ein "A" gezogen wurde und dann, im zweiten Zug nach diesem "A", ein "N".
Also kann man schreiben:
"AN" = "A" 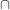 ("AN" | "A") ("AN" | "A")
(anstelle des 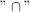 könnte man ev. auch ein könnte man ev. auch ein 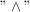 für das logische "und" setzen) für das logische "und" setzen)
Die obige Gleichung
P("AN") = P("A") *P("AN" | "A")
kann man dann auch so schreiben:
P("AN" | "A") = 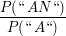 = = 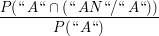
siehe auch: ![Link auf "http://de.wikipedia.org/wiki/Bedingte_Wahrscheinlichkeit" [link]](/images/popup.gif) Wikipedia Wikipedia
| 