SonstAnalysis
Gegeben sei eine ganz-rationale Funktion dritten Grades f sowie eine Gerade g, die den Graphen von f in drei Punkten mit den Abszissen 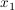 , ,  , , 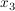 schneidet. schneidet.
(a) Die Wendestelle 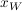 lässt sich in einfacher Weise aus lässt sich in einfacher Weise aus 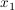 , ,  und und 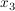 berechnen. Wie lautet die Formel? berechnen. Wie lautet die Formel?
(b) Wenn die Abszissen 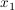 und und  sich einer Stelle sich einer Stelle 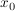 nähern, wird die Gerade g zur Tangente durch ( nähern, wird die Gerade g zur Tangente durch (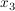 ,0). Wie lautet die Beziehung zwischen ,0). Wie lautet die Beziehung zwischen 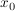 , , 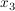 und und 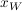 jetzt? jetzt?
(c) Ist die Gerade g die x-Achse, so sind 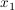 , ,  und und 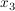 die Nullstellen von f, und der Berührpunkt der Tangente durch ( die Nullstellen von f, und der Berührpunkt der Tangente durch (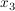 ,0) hat besonders bemerkenswerte Koordinaten. ,0) hat besonders bemerkenswerte Koordinaten.
Untersuche zunächst ein konkretes Beispiel, etwa  , die Gerade g verbinde die Punkte (-15,?), (15,?) auf dem Graphen von f. Stelle dann für die Teile (a), (b) und (c) allgemeine Behauptungen auf und versuche, diese zu beweisen. , die Gerade g verbinde die Punkte (-15,?), (15,?) auf dem Graphen von f. Stelle dann für die Teile (a), (b) und (c) allgemeine Behauptungen auf und versuche, diese zu beweisen.
Fragen zur Lösung dieser Aufgabe stellst du am besten im ![Link auf "https://matheraum.de" [link]](/images/popup.gif) MatheRaum. MatheRaum.
| 