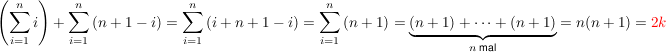PotenzsummeSatz Potenzsummenformeln
Schule und Universität
Eine Potenzsumme ist eine Summe der Form
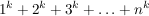
Geschlossener Term für bestimmte Potenzsummen:
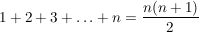
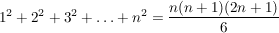
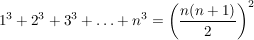
Beweis.
Wird im allgemeinen mit vollständiger Induktion geführt.
Auch wenn man es im Internet bestimmt irgendwo nachlesen kann, wollte ich nochmal bemerken, daß man die einfache Summenformel 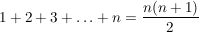 auch ohne Induktion direkt herleiten kann auch ohne Induktion direkt herleiten kann
(Bei den Summenformeln für höhere Potenzen ist das wohl nicht mehr so einfach).
Angenommen wir wüßten für jedes n der Summe
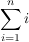
welcher Wert k für diese Summe rauskommen müßte. Dann gilt doch:
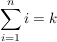
Und wenn wir nun auf beiden Seiten mit 2 multiplizieren, ändert sich doch auch nichts, oder?
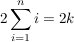
Aber schreiben wir die Summe doch mal aus:
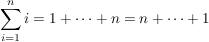
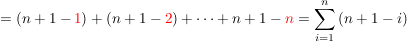
Und das war letztlich Gauss' wunderschöne Idee, den nun gilt doch:
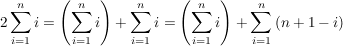
Und wegen dem Kommutativgesetz der Addition
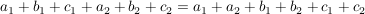
können wir nun die obigen Summen zusammenfassen:
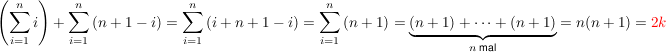
Und jetzt nur noch eine letzte Umformung:

Das war's.
|