LogarithmusDefinition
Für positive Zahlen b,x (also 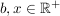 ) ist der 'Logarithmus' definiert als: ) ist der 'Logarithmus' definiert als:
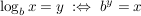 ("Bestimmungsgleichung des Logarithmus") ("Bestimmungsgleichung des Logarithmus")
Es ist also 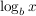 diejenige Zahl, mit der man die Basis b potenzieren muß um x zu erhalten. diejenige Zahl, mit der man die Basis b potenzieren muß um x zu erhalten.
Für bestimmte Basen b gibt es spezielle Schreibweisen:
- Zur Basis b=10:
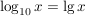
- Zur Basis b=e:
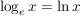 ("logarithmus naturalis") (e ist die Eulersche Zahl) ("logarithmus naturalis") (e ist die Eulersche Zahl)
- Zur Basis b=2:
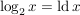 ("logarithmus dualis") ("logarithmus dualis")
Beispiel:
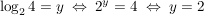
Logarithmusgesetze
Diese Gesetze folgen direkt aus der Definition des Logarithmus:
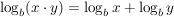 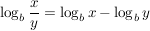 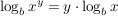 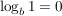 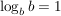 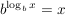 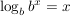
Beispiele für die Anwendung der Rechengesetze
Zeigen Sie, dass für a, b > 0 gilt: 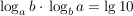
Nach der Definition des Logarithmus gilt:
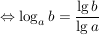 und analog 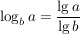
Damit gilt dann: 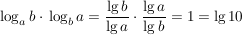
Beweise der Logarithmusgesetze
| 