Kleinsche VierergruppeDefinition Kleinsche Vierergruppe
Universität
Es sei 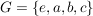 eine Gruppe mit neutralem Element eine Gruppe mit neutralem Element  und es gelte und es gelte
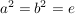 . .
Da in jeder Zeile und jeder Spalte der Gruppentafel jedes Element genau einmal auftauchen muss, ist die Gruppenstruktur von 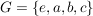 durch diese Forderung bereits eindeutig festgelegt: durch diese Forderung bereits eindeutig festgelegt:

Man überzeugt sich, dass es sich tatsächlich um eine Gruppe handelt, indem man das Assoziativgesetz überprüft. Unten wird eine "Realisierung" der vorstehenden Struktur angegeben, für die das Assoziativgesetz trivialerweise erfüllt ist.
Die angegebene Gruppe 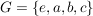 mit mit 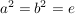 heißt Kleinsche Vierergruppe (benannt nach Felix Klein, 1849-1925). heißt Kleinsche Vierergruppe (benannt nach Felix Klein, 1849-1925).
Quelle: isbn3446130799
Fortsetzung folgt später...
| 
