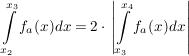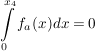Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
Sigrid Sprock
Marc O. Sandlus | www.matheraum.de
Vorbereitung auf das Zentralabitur in Mathematik in NRW
Aufgabenblatt 1
Abgabe: Fr 10.07.2009 16:00 | 22.09.2006 | | Aufgabe 1 | Flächenstrategien
Gegeben sind die Funktionen 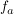 mit mit 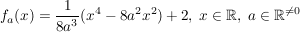 . .
a) Untersuchen Sie für 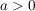 den Graphen zu den Graphen zu 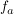 auf Symmetrie sowie auf sein Verhalten für auf Symmetrie sowie auf sein Verhalten für 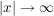 . Bestimmen Sie die Extrem- und Wendepunkte des Graphen in Abhängigkeit von . Bestimmen Sie die Extrem- und Wendepunkte des Graphen in Abhängigkeit von  . .
b)
1. Bestimmen Sie denjenigen Wert von  , für den der zu , für den der zu 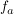 gehörende Graph einen Extrempunkt auf der x-Achse hat. gehörende Graph einen Extrempunkt auf der x-Achse hat.
2. Beschreiben Sie den Verlauf der Graphen für negative Werte  und begründen Sie Ihre Aussage. und begründen Sie Ihre Aussage.
3. Bestimmen Sie die Anzahl der Nullstellen von 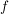 in Abhängigkeit von in Abhängigkeit von  . .
4. Ermitteln Sie alle Werte für  , so dass der Graph zu , so dass der Graph zu 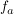 durch den Punkt durch den Punkt  verläuft. verläuft.
5. Alle Graphen in der Zeichnung unten gehören zur Schar 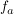 . Geben Sie jeweils das passende . Geben Sie jeweils das passende  an bzw. den Bereich, aus dem der zugehörige Wert von an bzw. den Bereich, aus dem der zugehörige Wert von  stammt, und begründen Sie Ihre Zuordnung. stammt, und begründen Sie Ihre Zuordnung.
![[Dateianhang]](uploads/forum/00180373/forum-i00180373-n001.png)
c) Es soll die folgende Problemstellung bearbeitet werden:
"Bestimmen Sie den Wert von  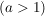 , für den der Inhalt der vom Graphen zu , für den der Inhalt der vom Graphen zu 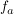 und der x-Achse oberhalb der x-Achse eingeschlossenen Fläche gleich dem Inhalt der Flächen ist, die die x-Achse und der Graph unterhalb der x-Achse umschließen." und der x-Achse oberhalb der x-Achse eingeschlossenen Fläche gleich dem Inhalt der Flächen ist, die die x-Achse und der Graph unterhalb der x-Achse umschließen."
Zur Lösung werden die Vorschläge V 1 und V 2 gemacht:
V1: Ich bestimme die Nullstellen 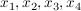 mit mit 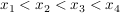 und löse die Gleichung und löse die Gleichung
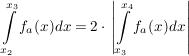 . .
V2: Ich bestimme die Nullstellen 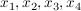 mit mit 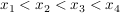 und löse die Gleichung und löse die Gleichung
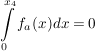 . .
Beurteilen Sie diese beiden Vorschläge. |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|

![[Dateianhang]](uploads/forum/00180373/forum-i00180373-n001.png)