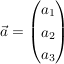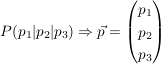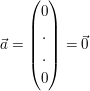| Mach mit! und verbessere/erweitere diesen Artikel! | | Artikel • Seite bearbeiten • Versionen/Autoren | Vektor
Schule
Geometrische Definition:
- Ein Vektor ist eine Klasse von Verschiebungen oder Pfeilen, die die gleiche Länge, Richtung und Orientierung haben.
- Ein Vektor ist also eine Größe, die aufgrund der Angabe von Maßzahl (Länge) und Richtung vollständig beschrieben ist. In physikalischen Anwendungen wird zusätzlich eine Einheit mit angegeben.
- Die Länge eines Vektors wird sein Betrag genannt und durch das Symbol
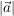 oder a dargestellt. Der Betrag eines Vektors ist stets positiv: oder a dargestellt. Der Betrag eines Vektors ist stets positiv:

- Im anschaulichen Raum
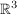 kann man sich einen Vektor vorstellen als ein Tripel von reellen Zahlen: kann man sich einen Vektor vorstellen als ein Tripel von reellen Zahlen: 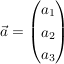 . .
- Die reellen Zahlen
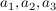 nennt man die Komponenten des Vektors. nennt man die Komponenten des Vektors.
- Mit Vektoren kann man rechnen: siehe Vektorrechnung
spezielle Vektoren:
- Ortsvektor
Der Vektor, der vom Koordinatenursprung zu einem bestimmten Punkt verläuft:
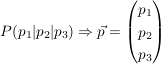
- Richtungsvektor / Spannvektor
nennt man einen Vektor, der die Richtung einer Geraden bestimmt.
Durch zwei Richtungsvektoren wird eine Ebene aufgespannt: darum bezeichnet man Richtungsvektoren auch als Spannvektoren.
- Einheitsvektor
nennt man einen Vektor der Länge Eins, 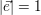 . .
- Normierter Vektor
Man erhält den auf Eins normierten Vektor, indem man den Vektor 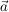 mit dem Kehrwert seiner Länge multipliziert: mit dem Kehrwert seiner Länge multipliziert:

- Nullvektor
Der Nullvektor ist ein Vektor, dessen sämtliche Komponenten 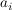 den Wert Null besitzen den Wert Null besitzen
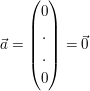
- Gegenvektor, auch inverser Vektor
Der Gegenvektor zum Vektor 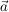 besitzt den gleichen Betrag, jedoch die entgegengesetzte Richtung zu besitzt den gleichen Betrag, jedoch die entgegengesetzte Richtung zu 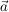
Universität
Abstrakte Definition:
Ein Vektor 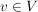 ist ein Element eines Vektorraumes ist ein Element eines Vektorraumes 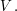
![Link auf "http://de.wikipedia.org/wiki/Vektor" [link]](/images/popup.gif) Vektor-Artikel der Wikipedia Vektor-Artikel der Wikipedia
![Link auf "http://www.mathe-online.at/mathint/vect1/i.html#Vektor" [link]](/images/popup.gif) Vektor-Artikel in mathe-online.at Vektor-Artikel in mathe-online.at
| | Erstellt: Mi 08.09.2004 von Marc | | Letzte Änderung: Do 06.06.2013 um 15:38 von Marcel | | Weitere Autoren: Herby, informix | | | Artikel • Seite bearbeiten • Versionen/Autoren • Titel ändern • Artikel löschen • Quelltext |
|